Chapter 9A Conic Sections, Parametrized Curves, and Polar Coordinates
| Page | Description | Equation |
|---|---|---|
| 710 |
|
\[ x^2+y^2=a^2 \] |
| 710 |
|
\[ (x-h)^2+(y-k)^2=a^2 \] |
| 711 |
|
\[ \] |
| 714 |
semimajor axis: $a$ semiminor axis: $b$ Center-to-focus distance: \[ c=\sqrt{a^2-b^2} \] Foci: \( (\pm\,c,0) \) Vertices: \( (\pm\,a,0) \) |
\[ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \] where $a\gt b.$ |
| 714 |
semimajor axis: $a$ semiminor axis: $b$ Center-to-focus distance: \[ c=\sqrt{a^2-b^2} \] Foci: \( (0,\pm\,c) \) Vertices: \( (0,\pm\,a) \) |
\[ \frac{x^2}{b^2}+\frac{y^2}{a^2}=1 \] where $a\gt b.$ |
| 716 |
|
\[ \] |
| 723 |
|
\[ \] |
| 724 |
|
\[ \] |
| 725 |
|
\[ \] |
| 725 |
|
\[ \] |
| 728 |
|
\[ \] |
| 728 |
|
\[ \] |
| 729 |
|
\[ \] |
| 729 |
|
\[ \cot2\alpha=\frac{A-C}{B} \] |
| 729 |
|
\[ \tan2\alpha=\frac{B}{A-C} \] |
| 731 |
|
\[ \begin{array}{cl} \textbf{Discriminant}&\textbf{Graph}\\ B^2-4AC=0&\text{parabola}\\ B^2-4AC\lt0&\text{ellipse}\\ B^2-4AC\gt0&\text{hyperbola} \end{array} \] |
Notes |
|
| Page | Notes |
|---|---|
| 709 |
Definition.
A |
| 711 |
Definition.
A set that consists of all the points in a plane
equidistant from a given fixed point and a given
fixed line in the plane is a
|
| 712 |
Definition.
An
Referring to fig 9.5, assume we drew this figure by fixing tacks at the arbitrary points $F_1$ and $F_2$ and winding a fixed-length string around them and a pencil at $P(x,y),$ so that the loop of string is depicted by the red lines in the figure. Since the length of the string, $F_1F_2+PF_1+PF_2,$ and the segment $F_1F_2,$ are both constant, then their difference, $PF_1+PF_2,$ is constant, too. However, $PF_1+PF_2$ is the sum of the distance from $P$ to two fixed points $F_1$ and $F_2.$ Therefore, by definition, the set of points $\{P(x,y)\}$ traced by the pencil is an ellipse, and $F_1$ and $F_2$ are its foci. |
| 713 |
Definition.
The line through the foci of an ellipse is its
|
| 713 | Proof. Referring to fig 9.7, we shall prove the caption. The distance formula gives \[ PF_1 = \sqrt{(x+c)^2+y^2} \] \[ PF_2 = \sqrt{(x-c)^2+y^2} \] Furthermore, at $P(a,0),$ $PF_1=OF_1+OP=\abs{-c}+a=c+a$ and $PF_2=OF_2-OP=a-c$ so that $PF_1+PF_2$$=(c+a)+(a-c)$$=2a.$ Since, $PF_1+PF_2$ is constant for all $P,$ we obtain \begin{equation} \label{eq1} PF_1+PF_2=2a \end{equation} Combining the previous equations, we have \[ \sqrt{(x+c)^2+y^2} +\sqrt{(x-c)^2+y^2} =2a \] From this equation we obtain \begin{equation} \label{eq2} \frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1 \end{equation} by way of some lengthy algebra as follows: \[ \sqrt{(x+c)^2+y^2} =2a -\sqrt{(x-c)^2+y^2} \] \[ (x+c)^2+y^2 =\left(2a-\sqrt{(x-c)^2+y^2}\right)^2 \] \[ (x+c)^2+y^2 =4a^2-4a\sqrt{(x-c)^2+y^2}+(x-c)^2+y^2 \] \[ \left[\frac{(x+c)^2-(x-c)^2-4a^2}{-4a}\right]^2 =(x-c)^2+y^2 \] \[ \left(\frac{4cx-4a^2}{-4a}\right)^2 =(x-c)^2+y^2 \] \[ a^2+\frac{c^2x^2}{a^2} =x^2+c^2+y^2 \] \[ (a^2-c^2)+\frac{c^2}{a^2}x^2-x^2 =y^2 \] \[ (a^2-c^2)+x^2\left(\frac{c^2}{a^2}-1\right) =y^2 \] \[ (a^2-c^2)+x^2\left(\frac{c^2-a^2}{a^2}\right) =y^2 \] \[ (a^2-c^2)-x^2\left(\frac{a^2-c^2}{a^2}\right) =y^2 \] \[ (a^2-c^2)\left(1-\frac{x^2}{a^2}\right) =y^2 \] \[ 1-\frac{x^2}{a^2} =\frac{y^2}{a^2-c^2} \] \[ \frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1\qquad \blacksquare \] To conclude the proof, we note that $b^2=a^2-c^2.$ To see that this is so, observe that $PF_1=PF_2$ at $P(0,b).$ Then, $2a=2PF_1$ at that point. Therefore, $a=PF_1,$ the hypotenuse of $\triangle abc.$ Since $a,b,c$ are constant for all $P,$ not just at $P(0,b),$ it follows that \begin{equation} \label{eq4} a^2=b^2+c^2 \end{equation} for all $P(x,y).$ Therefore, equation (\ref{eq2}) can be simplified to \begin{equation} \label{eq3} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \end{equation} and the proof is complete. |
| 713 |
Definition.
The |
| 715 |
Definition.
A
|
| 715 |
Definition.
The line through the foci of a hyperbola is the
|
| 716 |
|
| 716 |
Definition.
If an ellipse is revolved about its major axis
to generate a surface, the surface is called an
|
| 718 |
Definition.
|
| 730 |
Definition.
|
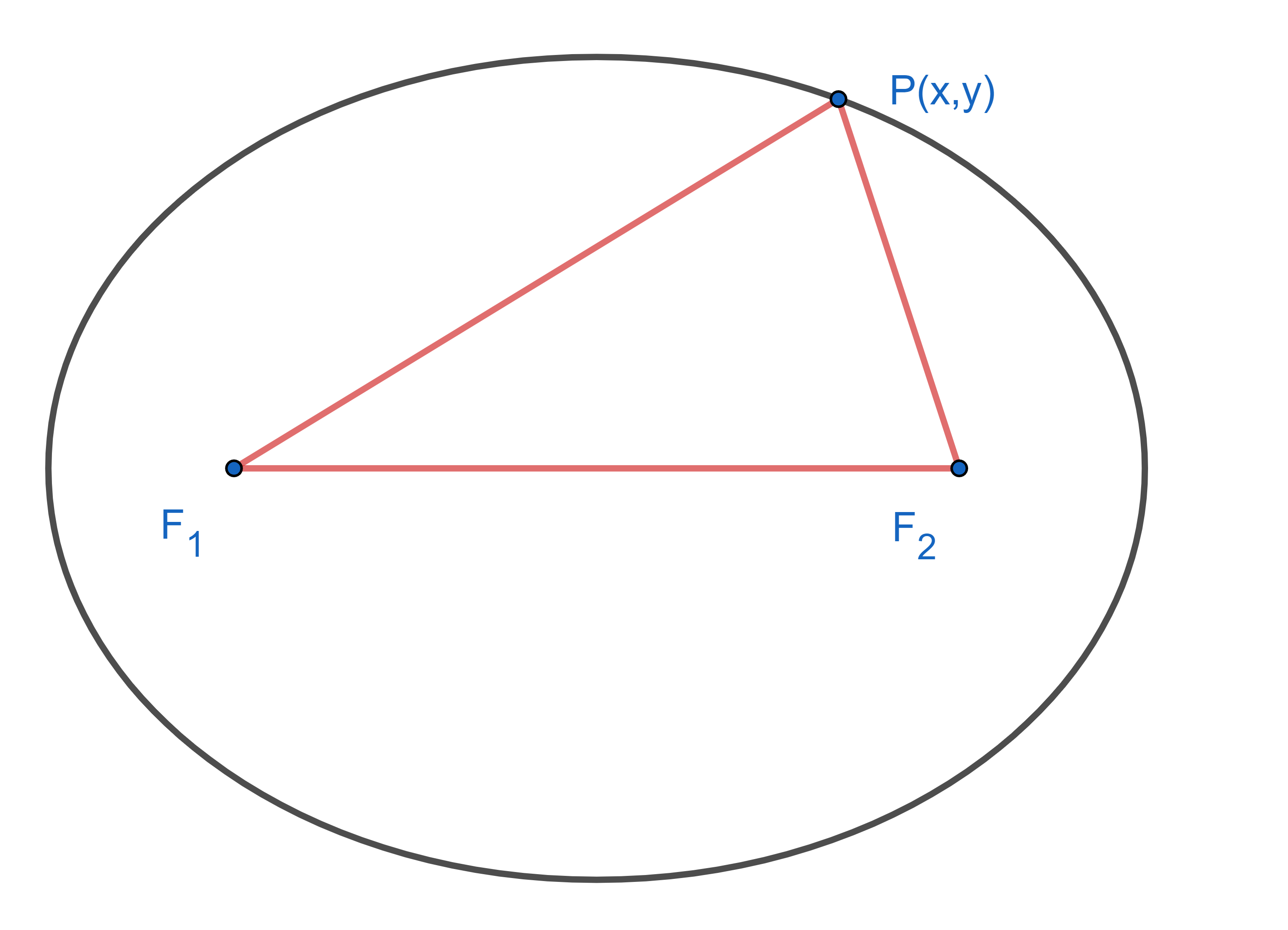 Fig 9.7 An ellipse.
\(
PF_1+PF_2
\)
is constant.
Fig 9.7 An ellipse.
\(
PF_1+PF_2
\)
is constant.
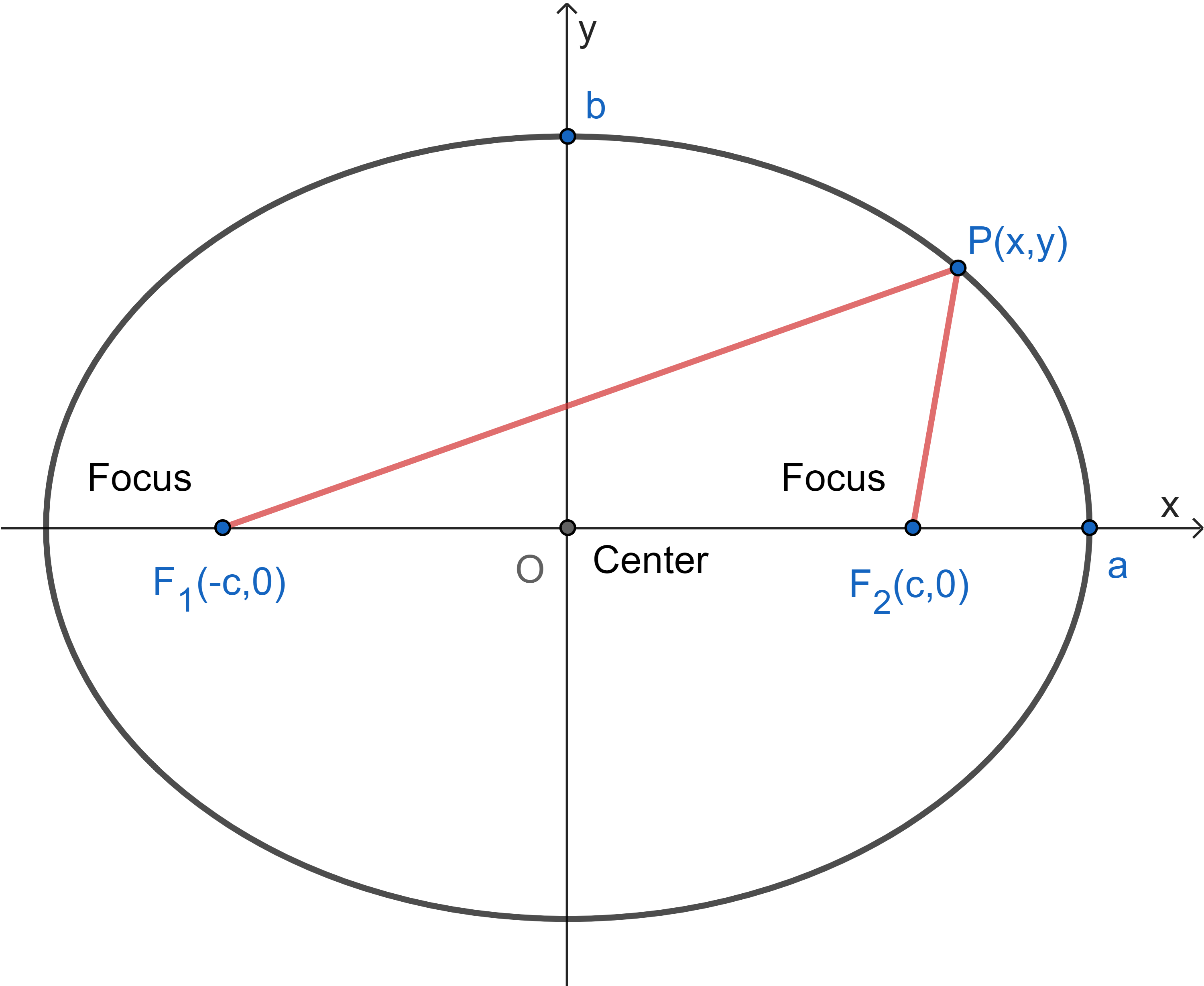 Fig 9.7 Ellipse defined by
\(
PF_1+PF_2=2a
\)
is the graph of the equation
\(
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.
\)
Fig 9.7 Ellipse defined by
\(
PF_1+PF_2=2a
\)
is the graph of the equation
\(
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.
\)