Page
Description
Equation
292 polynomial function of degree $n.$ \begin{align*} P(x) &=a_nx^n+a_{n-1}x^{n-1}\\ &+a_{n-2}x^{n-2}+\cdots\\ &+a_2x^2+a_1x+a_0 \end{align*} 293 division algorithm for polynomials yields a quotient polynomial $Q(x)$ and a remainder polynomial $R(x)$ of degree less than that of the divisor $D(x)$, \[ \frac{P(x)}{D(x)}=Q(x)+\frac {R(x)}{D(x)}. \] 295 synthetic division A shortcut that may be used to divide a polynomial of degree $n\geq1$ by a first degree polynomial $x-r$. The essential data from the long division process by eliminating any power of $x$ or coefficient that is a duplicate of that directly above it. Also replacing the divisor $x-r$ by synthetic division $r$ so that it can be add rather than subtract columns. 297 remainder theorem When a polynomial $P(x)$ is divided by $x-r,$ the remainder is $P(r)$. 298 zero, root of a polynomial equation If $P(x)$ is a polynomial and $r$ is a constant such that $P(r)=0$, lets say $r$ is a zero of the polynomial function $P$ or a root of the polynomial equation $P(x)=0.$ Any real zero of a function $P$ represents an $x$-intercept of the graph of $P$. 302 factor theorem A first-degree polynomial $x-r$ is a factor of a polynomial $P(x)$ if and only if $P(r)=0,$ or equivalently, if and only if $r$ is a zero of $P$. 303 fundamental theorem of algebra Every polynomial function $P$ of degree $n\geq1$ has at least one zero in the set of complex numbers. 304 extension of the fundamental theorem Every polynomial function $P$ of degree $n\geq1$ can be expressed as the product of $n$ linear factors and, consquently, $P$ has exactly $n$ zeros in the set of complex numbers. 304 zero of multiplicity $k$ If a linear factor $x-r$ appears $k$ times, then $r$ is zero of multiplicity $k$. 307 conjugate pair theorem If $P$ is a polynomial function of degree $n\geq1$ with real coefficients, and if the imaginary number $a+bi$ is a zero of $P$, then its conjugate $a-bi$ is also a zero of $P$. 307 two consequences of conjugate pair theorem
  1. A polynomial function with real coeffcients of odd degree must have at least one real zero. In fact, such a polynomial function must have an odd number of real zeros.
  2. A polynomial function with real coeffcients of even degree must have either an even number of real zero or no real zero at all.
311 rational zero theorem Let $P(x)$ be a polynomial function with integer coefficients and with $a_n\neq0,\ a_0\neq0.$ If the rational number $b/c,$ in lowest terms, is a zero of $P,$ then $b$ must be a factor of the constant term $a_0,$ and $c$ must be a factor of then coefficient of the highest degree term $a_n.$ 312 Descartes' rule of signs If $P(x)$ is a polynomial with real coefficient and is written in descending powers of $x,$ then
  1. The number of positive real zeros of $P$ either is equal to the number of variations in sign of $P(x)$ or is less than this number by an even number.
  2. The number of negative real zeros of $P$ either is equal to the number of variations in sign of $P(-x)$ or is less than this number by an even number.
314 upper and lower bound rule If $P(x)$ is a polynomial with real coeffcients and is written in descending powers of $x$ with a positive leading coeffcients, then
  1. If $P(x)$ is divided synthetically by $x-r,$ where $r\gt0,$ and all numbers in the final row of the synthetic division are nonegative, then $r$ is an upper bound for the real zeros of $P.$
  2. If $P(x)$ is divided synthetically by $x-r,$ where $r\lt0,$ and the numbers in the final row of the synthetic division alternate sign (are alternately nonpositive and nonegative), then $r$ is a lower bound for the real zero $P.$
Note. The number $0$ in the final row of the synthetic division may be considered either positive or negative, as needed. 315 general procedure for finding rational zeros The rational zeros of a polynomial function $P$ with integer coefficients and of degree $n\gt3$ can be found as follows:
  1. Use the rational zero theorem to list all possible rational zeros.
  2. Use Descartes' rule of signs to determine the number of positve and negative real zeros.
  3. Use synthetic division along with the upper and lower cound rule to find a rational zero $r$ from the possible zeros listed in step $1$.
  4. Use the rational zero from step $3$ to write.
\[ P(x)=(x-r)Q(x) \] and find the rational zeros of $Q,$ repeating the previous steps if necessary, until all rational zeros are found. 323 opposite sign property If $P(x)$ is a polynomial with real coefficients and if, for the real numbers $a$ and $b$, $P(a)$ and $P(b)$ have opposite signs, then there exists at least one real zero between $a$ and $b$. 324 method of successive approximations If $P(x)$ has one real zero in the interval $[a,b],$ where $a$ and $b$ are consecutive integers, then this zero can be approximated as follows:
  1. Divide the interval $[a,b]$ into ten parts to form ten equal subintervals.
  2. Determine the subintercal in step $1$ where $P(x)$ changes sign.
  3. Divide the interval found in step $2$ into ten equal parts to form ten sub-intervals.
  4. Determine the subinterval in step $3$ where $P(x)$ changes sign.
  5. Continue the process until the desired accuracy is achieved.
327 general procedure for finding real zeros If $P$ is a polynomial function with integer coefficients and of degree $n\gt3,$ then the rational zeros of $P$ can be found exactly and the irrational zeros of $P$ can be found approximately as follows:
  1. Find all the rational zeros $r_1\ldots r_k$ by using the procedure outline in Section 5.3.
  2. Use the rational zeros from step 1 to write \[ P(x)=(x-r_1)(x-r_2)\\ \cdots(x-r_k)Q(x) \] then use Descartes' rule of signs to determine if $Q(x)$ has any positive or negative irrartional zeros.
  3. Use synthetic divison along with the opposite sign property to determine an interval on which each irrational zero is located.
  4. Use the method of successive approximations or a calculator with graphing capabilities to approximate the irrational zeros to the desired degree of accuracy.
332 left and right behavior of graph of a polynomial function The graph of a polynomial function $P$ eventually rises or falls depending on
  • the sign of its leading coefficient $a_n$, and
  • whether $n$ is even or odd
334 relative extrema If $P$ is a polynomial function of degree $n$ with real coeffcients, then the number of relative extrema either is equal to $n-1$ or is less than this number by an even number. 335 general procedure for graphing a polynomial function To sketch the graph of a polynomial function $P$ with real coeffcients and of degree $n\gt3,$ proceed as follows:
  1. Determine the left and right behavior of the graph. Then determine the possible shapes for the middle of the gragh by considering relative extrema.
  2. Determine the $y$-intercept by evaluating $P(0).$
  3. Determine the real zeros of the function $P$. These real zeros are the $x$-intercepts for the graph of $P.$
  4. Determine the intervals into which the $x$-intercepts divide the $x$-axis. Then select a few values of $x$ from each of these intervals and determine their corresponding outputs, $P(x).$
  5. Plot the points gathered in steps 2-4, and connect the points to form a smooth curve.
336 tangency If $r$ is a zero of multiplicity $k,$ with $k\gt2,$ for a polynomial function $P,$ then the graph of $P$ is tangent to the $x$-axis at $x=r.$ 341 rational functions A function where $P(x)$ and $D(x)$ are polynomials and $D(x)\neq0$ \[ f(x)=\frac{P(x)}{D(x)} \] 342 vertical asymptotes of a rational function \[ f(x)=\frac{P(x)}{D(x)} \] where $\frac{P(x)}{D(x)}$ is reduced to lowest terms and find the real zeros of $D.$ If $a$ is a real zero of $D,$ then the vertical line $x=a$ is a vertical asymptote of the graph of $f.$ 344 horizontal asymptote The line $y=b$ is a horizontal asymptote of the graph of a rational function $f$ if at least one of the following statements is true.
  • \[ x\rightarrow\infty,\ f(x)\rightarrow b^+ \]
  • \[ x\rightarrow\infty,\ f(x)\rightarrow b^- \]
  • \[ x\rightarrow\infty,\ f(x)\rightarrow b^+ \]
  • \[ x\rightarrow\infty,\ f(x)\rightarrow b^- \]
344 rules for the existence of horizontal asymptote
  1. One horizontal asymptote if the degree of $P(x)$ is less than or equal to the degree of $D(x).$
  2. No horizontal asymptote if the degree of $P(x)$ is greater than the degree of $D(x).$
347 general procedure for graphing a rational function To graph a rational function \[ f(x)=\frac {P(x)}{D(x)} \] where the degree of $P(x)$ is less than or equal to the degree of $D(x)$ and $P(x)/D(x)$ is reduced to lowest terms, proceed as follows:
  • Step 1. Find the vertical asymptote(s) of the graph of $f$ and determine the appearance of the graph of $f$ as $x$ approaches each vertical asymptote from the left and from the right.
  • Step 2. Find the horizontal asymptote of the graph of $f$ and determine the appearance of the graph of $f$ as $|x|\rightarrow\infty.$
  • Step 3.
    • a. Find the $x$-intercept for the graph of $f.$
    • b. Find the $y$-intercept for the graph of $f.$
    • c. Determine whether the graph crosses its horizontal asymptote.
  • Step 4. Plot the points from step 3 and, if necessary, plot a few additional points. Then sketch the graph.
348 oblique asymptote An asymptote that is neither a vertical nor horizontal line. 350 rational functions with common factors To graph a rational function with common factors, it starts with reducing $P(x)/D(x)$ to lowest term. Sometimes it may have "holes", to indicate that $f$ is not a continuous function. 350 average cost function. Let $T=$ total cost of producing $x$ units. Then, \[ C(x)=\frac{T(x)}{x} \] 356 partial fraction decomposition, partial fraction If $P(x)/D(x)$ is a rational expression reduced to lowest terms, and if the degree of $P(x)$ is less than the degree of $D(x),$ then $P(x)/D(x)$ can be written as a partial fraction decomposition of the form \[ \frac{P(x)}{D(x)}=F_1(x)+F_2(x)+\\ \cdots+F_n(x) \] where each partial fraction $F_i(x),$ $i=1\ldots n,$ has the form \[ \frac{A}{(a+bx)^n} \] or \[ \frac{Bx+C}{(px^2+qx+r)^m} \] for some real numbers $A,$ $B,$ and $C$ and nonegative integers $m$ and $n.$ 356 irreducible quadratic factor An irreducible quadratic factor is prime over the reals. $$ \frac{Bx+C}{(px^2+qx+r)^m} $$ 356 four cases of partial fraction decomposition
  1. Distinct linear factors in the denominator
  2. Repeated linear facotrs in the denominator
  3. Distinct irreducible quadratic factors in the denominator
  4. Repeated irreducible quadratic factors in the denominator
357 distinct linear factors \[ \frac {A}{ax+b} \] where $A$ is a constant to be determined. 358 repeated linear factors \[ \frac{A}{ax+b},\\ \frac{A}{(ax+b)^2},\\ \frac{A}{(ax+b)^3},\\ \ldots,\\ \frac{A}{(ax+b)^r} \] where $A_1\ldots A_r$ are constants to be determined. 360 distinct irreducible quadratic factors \[ \frac{Ax+B}{ax^2+bx+c} \] where $A$ and $B$ are constants to be determined. 361 repeated irreducible quadratic factors in the denominator \[ \frac{Ax+B}{ax^2+bx+c},\\ \frac{Ax+B}{(ax^2+bx+c)^2},\\ \ldots,\\ \frac{Ax+B}{(ax^2+bx+c)^r} \] where $A_1\ldots A_r$ and $B_1\ldots B_r$ are constants to be determined. 363 proper and improper rational functions Proper rational function is one in which the degree of the numerator is less than the degree of the denominator. Improper rational function is one in which the degree of the numerator is not less than the degree of the denominator.

Notes

Division Algorithm (Theorem)

For any polynomials $D$ and $P$ such that $D\left(x\right)\neq0$ and the degree of $D$ is less than the degree of $P,$ there exist unique polynomials $Q$ and $R$ such that the degree of $R$ is less than the degree of $D$ but greater than or equal to 0 and $P(x)=Q(x)D(x)+R(x).$

Remainder Theorem

For any number $x$ and $c$ such that $x\neq c$ and any polynomial $P,$ $P(x)=Q(x)(x-c)+P(c).$

Factorable polynomial

A polynomial $P\left(x\right)$ is factorable if there exist at least two polynomials $Q\left(x\right)$ and $D\left(x\right)$ such that $P\left(x\right)=Q\left(x\right)D\left(x\right).$

Prime polynomial

A polynomial is prime if and only if it is not factorable using integer coefficients.

Prime factorization, completely factored, polynomial

A polynomial is completely factored if and only if it is written as the product of prime polynomials with integer coefficients, except that monomial factors need not be factored. For instance, $6x^3$ doesn't have to be written out as $2\cdot3\cdot xxx.$

Note that a polynomial need not have integer coefficients to be prime. Thus, the stipulation that the prime factors have integer coefficients is not redundant.

Note that neither $(x-2)\left(x-\frac{1}{2}\right)$ nor $\frac{1}{2}(4x^2-5x+2)$ is a prime factorization of the polynomial $2x^2-\frac{5}{2}x+1,$ since $\frac{1}{2}$ is not an integer coefficient.

Some questions:

  • Does the trinomial just mentioned have a prime factorization?
  • Is every prime factorization of a polynomial unique, e.g. if $ab$ is a prime factorization of $p$ and $cd$ is a prime factorization of $p,$ then either $a=c$ and $b=d,$ or $a=d$ and $b=c$?
  • Does every polynomial have a prime factorization, or do polynomials exist that do not have one?

Factor Theorem

For any numbers $x$ and $c,$ and any polynomial $P,$ $x-c$ is a factor of $P(x)$ if and only if $P(c)=0.$

Factor Definition

For any real numbers $a$ and $b,$ $b$ is a factor of $a$ if and only if there is a number $c$ such that $a=bc.$

Factor Theorem; Remainder Theorem; Factors; Polynomials

Consider functions $y_1$ and $y_2$ shown below:


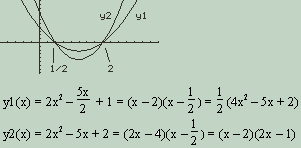
fig. 1. Two Polynomials

Notice in particular the following facts about these functions:

Two different factorizations for each polynomial, $y_1(x)$ and $y_2(x),$ are given. Two factors are common to both $y_1(x)$ and $y_2(x),$ namely, $(x-2)$ and $\left(x-\frac{1}{2}\right).$ $y_1$ and $y_2$ have the same zeros, namely, 2 and $\frac{1}{2}.$ This can be seen on the graphs where $y_1$ and $y_2$ intersect.

Now, suppose you were given the polynomial $y_2(x)$ to factor completely, and you were told its two zeros to help you. By the Fundamental theorem of Algebra, you would know that there were no other zeros, and by the Factor Theorem you would know that $(x-2)$ and $\left(x-\frac{1}{2}\right)$ were factors of $y_2(x).$

From this information, you might conclude that for all $x,$ $y_2(x)=(x-2)\left(x-\frac{1}{2}\right).$ Yet, if that were true, then for all $x,$ $y_2(x)=y_1(x),$ since $y_1(x)$ has an identical factorization (see graph above). This cannot be, since $y_1$ and $y_2$ are not equal, as can be seen from their graphs which do not coincide except at their zeros.

The reason for the error is that neither the Factor Theorem nor the Fundamental Theorem says that a polynomial of $n$ degree has n unique factors, or that a polynomial with n roots has $n$ unique factors. (Is this not true precisely when any of the zeros are not integers?)

The very example of $y_1(x)$ and $y_2(x)$ above defies these notions, since two factorizations are displayed for each polynomial. Furthermore, notice that $y_1(x)$ has no prime factorization. (Is this true? Neither factorizations given are prime, but does the polynomial have no prime factorization?) Still, the following sentences are equivalent:

  • $x-c$ is a factor of the polynomial $P.$
  • $c$ is a zero of the function $P.$
  • $c$ is a root of the equation $P(x)=0.$

The moral of the story is that given some or all of the zeros of a polynomial, one must use the Division Algorithm to find the complete factorization of the polynomial if either a) not all the zeros are given, or b) any of the zeros are not integers.

For each $c$ that is an integer and a zero of a polynomial, it is certain that the factor $x-c$ is part of the prime factorization. (Why? Since the prime factorization of a polynomial is unique? You haven’t read that claim anywhere, would need proof.) Therefore, any factor of the form $x-c,$ where $c$ is a zero and integer, could be used as the divisor in the division of the polynomial to find the remaining factors of its prime factorization.